A-Zero

# 地理参考系统及投影

# 地理参考系统描述

# 地球自然表面

地球的自然表面不是平整的、不规则的

# 大地水准面

地球表面的第一级逼近。假设当海水处于完全静止的平衡状态时，从海平面延伸到所有大陆下部

# 地球椭球体

地球表面的第二级逼近。是一个数学上定义的地球表面，它近似于大地水准面

# 大地基准面

地球表面的第三极逼近。由于不同的地区关心的位置不同，需要最大限度的贴合自己的那一部分，地球椭球体经过定位，定向，使其与自己国家的大地水准面最为贴合，这样就形成了不同的大地基准面
椭球体与大地基准面之间的关系是一对多的关系

# 常用的坐标系

# 参心大地坐标系(已经被淘汰)

基准面是大地基准面、区域基准面

  • 54坐标系：苏联的克拉索夫斯基椭球体
  • 80坐标系：指1980年西安坐标系，该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇

# 地心大地坐标系

  • WGS84坐标系（全球适用）
  • CGCS2000 与 WGS84 相差几个厘米，对于一般工程测量，可以认为二者是一致的

# 火星坐标系（GCJ-02）

出于国家安全考虑， 国内所有导航电子地图必须使用国家测绘局制定的加密坐标系统，即将一个真实的经纬度坐标加密成一个不正确的经纬度坐标

  • 标准坐标系：国外地图服务、iOS原生定位、天地图（属于CGCS2000，但可以等同于WGS84）
  • 火星偏移坐标系：Gogole地图、腾讯地图、高德地图等
  • 其他偏移坐标系：在火星坐标系上二次加密，如：百度地图（bd09）、搜狐搜狗地图

欧洲石油调查组织EPSG（European Petroleum Survey Group）

该组织负责专门维护地球上所有的测量坐标系统，并且给每组坐标系统都赋予了一个编号WKID

  • WGS84：4326（地理坐标系）
  • 2000国家大地坐标系（CGCS2000）:4490
  • 伪墨卡托投影：3857（投影坐标系）

# 地理参考坐标系（地理坐标系、GCS）

通常地图上使用的经纬度都为大地经纬度

地理参考坐标系

# 大地经纬度坐标系（大地坐标系、LBH）

基准面是地球椭球体，基准线是法线
经纬度表现形式有两种：度分秒(如113° 12' 34")、十进制(如113.534532)
转换公式：十进制=度+分/60+秒/3600

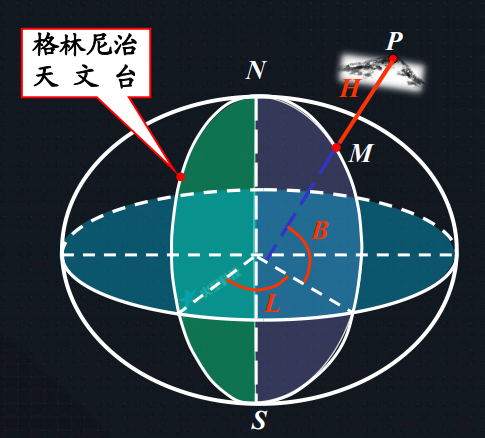
  • 大地经度 L：过地面点的子午面与起始子午面之间的夹角（0到正负180度）
  • 大地纬度 B：过地面点的法线与赤道面之间的夹角（0到正负90度）
  • 大地高度 H：地面点沿法线至参考椭球面的距离,可正可负

地理参考坐标系

# 空间直角坐标系（地心坐标系、XYZ）

基准面是地球椭球体，坐标原点位于参考椭球的中心，也称空间直角大地坐标系，常采用来确定地面点的三维坐标。空间坐标系的三个单位都是投影长度

  • Z轴：与椭球的旋转轴一致，指向参考椭球的北极
  • X轴：指向起始子午面与赤道的交点
  • Y轴：位于赤道面上，按右手系与X轴正交成90“夹角

空间直角坐标系

# 天文经纬度

基准面是大地水准面，基准线是铅垂线
天文经度：本初子午面与过观测点的子午面所夹的二面角（0到正负180度）
天文维度：过某点的铅垂线与赤道平面之间的夹角（0到正负90度）

# 地图投影坐标系（PCS）

地球椭球体表面是个面，而我们日常生活中的地图测量通常是二维平面，把曲面转化成平面的过程就是地图投影，单位是米

# 地图投影的类型

投影类型

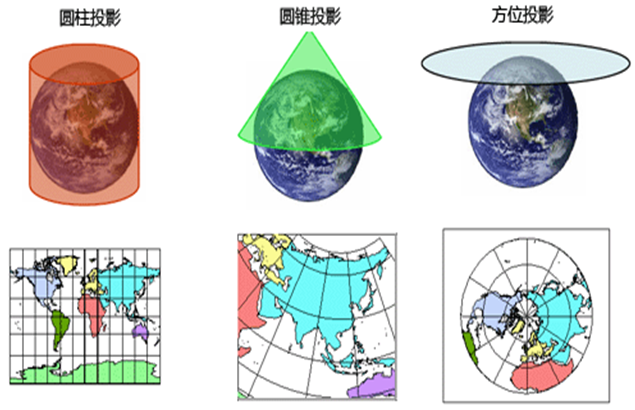
# 投影变形

通过地图投影并按比例尺缩小绘制成的地图，存在长度、面积、形状（角度）的变化

# 常用的地图投影

  • 墨卡托投影
    是正轴等角切圆柱投影，由每一点向各方向的长度比相等，即没有角度变形，而面积变形显著，越到高纬度，大小扭曲越严重，到两极会被放到无限大，墨卡托投影无法显示极地地区。常用于航天、航空
    墨卡托投影演示 (opens new window)

  • 伪墨卡托投影（球体墨卡托、Web Mercator）
    它是基于墨卡托投影的，在投影过程中，将表示地球的参考椭球体近似的作为正球体处理。谷歌地图、微软地图、百度地图、腾讯地图、高德地图等网络地图所使用的投影都是网络墨卡托投影

  • 高斯-克吕格投影（横轴墨卡托投影、横轴等角切圆柱投影）：
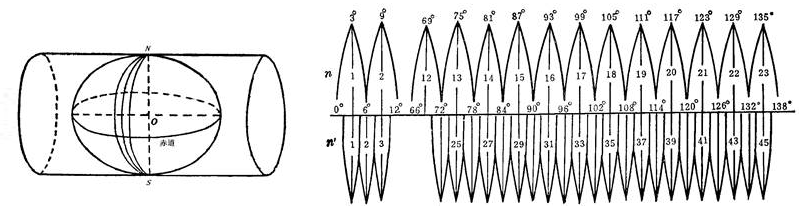
    高斯-克吕格投影
    6分带法

    • 特点

      • 中央经线和赤道投影为互相垂直的直线，且为投影的对称轴
      • 具有等角投影的性质
      • 中央经线投影后保持长度不变
      • 从0度子午线自西向东划分投影带

    • 投影变形的特点

      • 中央经线上没有变形
      • 同一条纬线上离中央经线越远变形越大
      • 同一条经线上维度越低变形越大

    • 6°分带法

      • 从格林威治零度经线起，自西向东，每6°分为一个投影带，分别用1-60予以标记
      • 东半球各投影带的中央经线位置为：L0=(6n-3)°
      • 西半球各投影带中央经线位置为：L0=(6n-3)°-360°

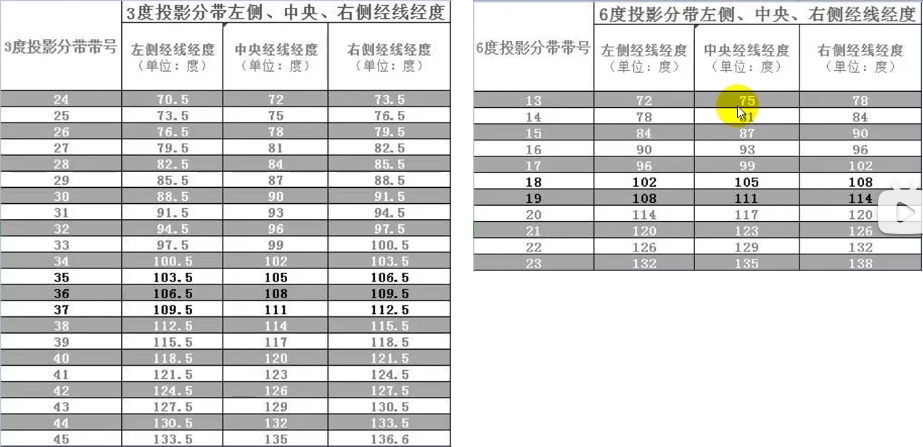
    • 3°分带法

      • 从东径1°30′算起，自西向东每3°为一带，将全球划分为120个投影带
      • 其中央经线的位置分别为3°、6°、9°……，180°，西经177°，……3°，0°
      • 这样分带的目的在于使6°带的中央经线均为3°带的中央经线 

    • 表示方法

      • CGCS2000 3 Degree GK CM 117E：3度分带，高斯克吕格投影，中央经线为117度
      • CGCS2000 3 Degree GK Zone 29：3度分带，高斯克吕格投影，分带号为29
      • CGCS2000 GK CM 117E：6度分带，高斯克吕格投影，中央经线为117度
      • CGCS2000 GK Zone 17：6度分带，高斯克吕格投影，分带号为17

    3Degree：3度分带，默认6度分带，GK：高斯克吕格投影，CM：中央经线，Zone：分带号

  • UTM投影（通用墨卡托投影，横轴等角割圆柱投影）
    可以改善高斯投影，圆柱割地球于南纬80度、北纬84度两条等高圈，投影后两条割线上没有变形，离两条割线越远变形越大，中央经线上长度比0.9996
    WGS84主要使用该投影方式
    UTM投影
    6分带法

    • 分为6度带和3度带，GIS常用的是6度带
    • 6度带从西经180度自西向东划分投影带，高斯-克吕格投影的第1带是UTM投影的第31带
    • 高斯-克吕格投影：我国6°分带13-23，3°分带24-45，UTM投影：6°分带43-53
    • 两投影的东伪偏移都是500公里，高斯-克吕格投影的北伪偏移是0，UTM北半球北伪偏移是0，南半球为10000公里

  • Lambert投影（兰勃特投影、正轴等角割圆锥投影）

    • 圆锥投影通常基于两条标准纬线，从而使其成为割投影，超过标准纬线的纬度间距将增加
    • 适用于小于（含) 1：100万的地图
    • 最适用于中纬度的一种投影。其描绘形状比描绘面积更准确
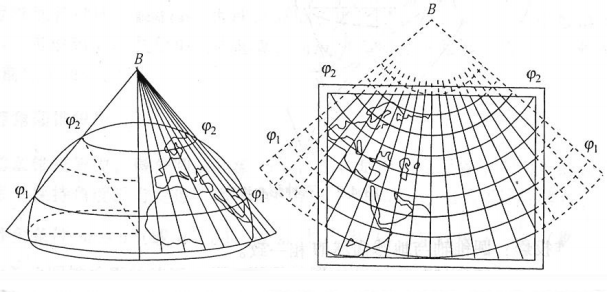
      兰勃特投影

比例尺

我国11种国家基本比例尺地形图中，除1：100万是等角圆锥投影外，其余都是高斯-克吕格投影

  • 1:500、1:1000、1:2000、1:5000、1:1万、1:2.5万、1:5万、1:10万、1:25万、1:50万、1:100万
  • 大中比例尺：1:50万及以上
  • 小比例尺：1:100万及以下
  • 1:2.5万到1:50万采用6度分带，1:1万及更大采用3度分带

# 坐标系转换

坐标系转换中主要是GCS转GCS，GCS转PCS就是投影，PCS转PCS是重投影
GCS转GCS这属于空间解析几何里的空间直角坐标系的移动、转换问题，还有个更高级的说法：仿射变换
欲将一个空间直角坐标系仿射到另一个坐标系的转换，需要进行平移、旋转、缩放三步，可以无序进行

# 地理空间对象及建模

# 地理空间对象

是地理实体和地理现象数字化的表达

# 地理实体

指具有相对固定的空间位置和空间关系，相对不变的属性

  • 离散地理实体：例如 井、道路、河流
  • 连续地理实体：例如 温度、湿度、浓度

# 地理现象

指具有相对固定的空间位置和空间关系，相对不变的属性，但是随着时间变化
被视为动态空间对象，记录空间、位置、属性的变化信息，进行时空变化建模

# 地理空间对象的特征

# 空间特征

位置、大小、形状（点、线、面）等的几何特征以及相邻地物的空间关系

# 属性特征

对空间对象进行描述

# 时间特征

根据时间变化的时空GIS

# 地理空间对象的数据类型

# 零维空间对象：点（Points）

  • 实体点（NE）:表示一个客观存在的对象
  • 标号点（NL）:用于定位标记
  • 节点（NO,NN）：线段的端点

# 一维空间对象：线（Polyline）

  • 线段
  • 弦列（LS）：表示相互连接的没有分支的线段
  • 弧
  • 拓扑连线：两个节点的拓扑连接，一节点的顺序可以确定其方向
  • 链：一个非相交线或弧的无分支而有方向的序列
  • 环：闭合的线段、弦列、弧，GT-环（有方向），G-环（没有方向）

# 二维空间对象：面（Polygon）

  • 内面：不包含边界
    内面
  • G-多边形
    G多边形
  • GT-多边形
    GT多边形

像元

它是一个二维的图素，不可再分的图像元素

# 三维空间对象：体

  • 体元：三维实体中不可再分割的元素
  • 标识体元：用于标识一个三维空间，类似二维的标识点
  • 三维组合空间目标：有二维空间目标组合（房屋），也可由三位体元构成
  • 体空间：三维空间实体

# 聚合空间对象：实体类型的组合

  • 图像：像元的集合
  • 栅格：同一网格或图像的一系列覆盖层
  • 层：按面分布的空间数据集合

# 地理空间建模（Geographic Space Modeling）

地理空间建模的二分法

  • 基于对象/实体的模型：离散的地理实体
  • 基于场的模型：连续的地理现象

# 地理空间对象的关系

研究当图形形状在弯曲、拉伸、收缩或其他方式扭曲下几何图形保持不变的属性
关注几何图形的之间的关系而不是他们的固定座标

# 空间关系

空间对象在拓扑变化（旋转、平移、缩放等）下保持不变的空间关系，即拓扑不变量，如相邻、联通。 几何结构相差较大的图形，其拓扑结构可能相同

# 空间拓扑关系的类型

  • 重合：基本几何体和比较几何体完全重合，具有相同维数的目标才存在重合关系
  • 包含：只有高维目标包含低维目标，或同维目标包含同维目标
  • 位于内部：基本几何体不能位于比自己维数低的比较几何体内
  • 相交：线与线，线与面，面与面都可能存在相交关系
  • 相离：基本几何体与比较集合体没有共享点
  • 重叠：基本几何体覆盖比较集合体，基本几何体和比较集合体必须是相同的维数
  • 相切：两个几何体又公共的边或点

# 方向关系

方向关系定量描述：以角度为参数进行描述
方向关系定性描述：以东南西北、前后左右相对位置为参数进行描述
代表性模型：锥形模型、方向关系矩阵模型

# 距离关系

点状目标间的平面距离算法
定量计算（欧氏距离）：最为广泛的使用方式
欧式距离算法
契比雪夫距离（切氏距离）：两点的X和Y坐标哪个差最大就是哪个
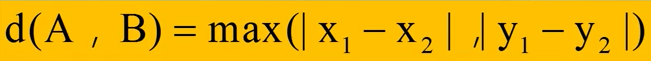
切氏距离算法
马氏距离（曼哈坦距离、街坊距离）：两点在坐标系上绝对轴距综合
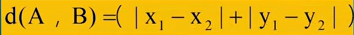
马氏距离算法

# 地理空间对象的结构

# 矢量数据结构

矢量数据结构是如同X,Y（或者X,Y,Z）坐标，利用点，线，面的形式来表达现实世界，具有定位明显，属性隐含的特点。由于矢量数据具有数据结构紧凑，冗余度低，表达精度高

# 要素 Feature

矢量数据的单个对象我们称之为“要素”，即矢量图层内是由多个要素（feature）构成的，而要素主要分为点、线、面等类型

# 矢量数据结构

  • 点：point [ x,y ] []表示元组
  • 线：polyline < point > <>表示列表
  • 面：polygon < point > <>表示列表
  • 区域：region { polygon } {}表示集合

# 拓扑矢量数据模型

矢量数据模型的描述信息包含：位置信息（x,y,z）、属性信息、空间关系信息

# 无空间拓扑关系的矢量数据模型

只记录空间目标的位置和属性信息，不记录它的拓扑关系，也称面条模型

# 栅格数据结构

栅格数据（瓦片模型）是以二维矩阵的形式来表示空间地物或现象分布的数据组织方式。每个矩阵单位称为一个栅格单元（cell）。栅格的每个数据表示地物或现象的属性数据
因此栅格数据有属性明显，定位隐含的特点
四叉树编码是最有效的栅格数据压缩编码方法之一，还能提高图形操作效率， 具有可变的分辨率
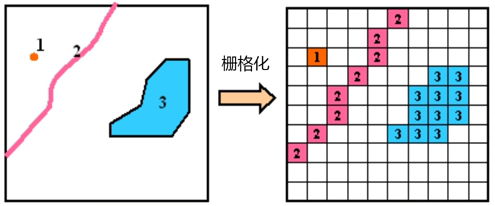
栅格数据结构

# 四叉树编码

# 基本思想

每个节点有4个分支，把一幅图像或一副栅格地图等分成四部分，逐块检查其网格值
如果某个子区的所有格网都含有相同的值，则子区不再分割，否则把子区再分割成四个子区域
递归分割直到每个子块都含有相同的灰度或属性值为止
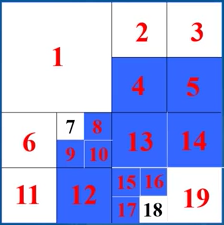
四叉树基本思想

# 常规四叉树

记录叶节点外，还要记录中间节点，节点之间的联系靠指针表达，也叫指针四叉树

节点记录的信息包含父节点指针，四个子节点指针，本节点灰度或属性值
增加了存储量和操作的复杂性

# 线性四叉树

只存储叶节点的信息

节点记录的信息包含位置，大小和灰度或属性值
叶节点的位置信息：遵照一定的规则对叶节点编号，这种编号成为地址码
地址码：其中隐含叶节点的位置信息

# 基于四进制的Morton码
  • 自上而下分裂建立四叉树，过程中逐步产生Morton码
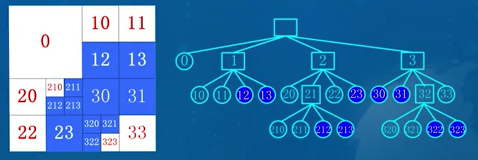
  • 首先计算每个网格的Morton码，然后扫描自下而上合并，建立四叉树 Morton1

# 切片（瓦片）地图

现在越来越多的地图服务用到瓦片技术，基本我们平常所接触的地图的底图都是瓦片地图。瓦片地图金字塔模型是一种多分辨率层次模型，从瓦片金字塔的底层到顶层，分辨率越来越低，但表示的地理范围不变

  • 瓦片分辨率为256××256
  • 最小的地图等级是0，此时世界地图只由一张瓦片组成
  • 具有唯一的瓦片等级（Z）和瓦片行列坐标编号（X, Y）
  • 瓦片等级越高，组成世界地图的瓦片数越多，可以展示的地图越详细
  • 某一瓦片等级地图的瓦片是由低一级的各瓦片切割成的4个瓦片组成，形成了瓦片金字塔 切片地图

# 分辨率和比例尺的关系

# 分辨率

在GIS中所提到的分辨率，也称地面分辨率（Ground Resolution）或空间分辨率（Spatial Resolution），表示一个像素（pixel）代表的地面实际距离。 以谷歌地图为例：在缩放级别为 1 时，图片大小为4个 256256 的图片，那么赤道上的空间分辨率为：地球赤道周长（实地距离）除以2562（像素大小）。其他纬度上的分辨率则为：纬度圈长度/512。 因此可以看出，分辨率取决于两个参数：纬度和缩放级别。缩放级别决定了像素的多少，纬度决定了地面距离的长短。 因此谷歌地图某视图下的分辨率计算公式为： 分辨率

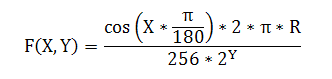
F(X,Y) # 地图分辨率（单位：米/像素）
X      # 纬度值
Y      # 缩放级别
R      # 常量 6378137，表示地球半径，单位：米

# 比例尺

比例尺通常以比率(如 1:10000 )来表示，表示图上距离与实地距离之比。例如 1:10000 表示图上 1cm 代表实际距离 10000cm，即100米。 由于比例尺起源较早，通常用（纸质）图上的距离衡量实际距离；而分辨率则通常用设备屏幕上的距离来衡量实际距离。而同一个地图视图，尺度是唯一的，比例尺和分辨率只不过是两种表示方法，因此它们是一一对应的。 比例尺与分辨率之间的换算公式如下： 比例尺

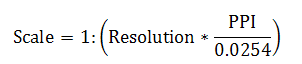
Scale # 地图比例尺
Resolution # 地图分辨率
PPI # 每英寸的像素点数

← 空间数据处理 →